对结合能的理解
一、核能
由于核子间存在强大的核力,所以核子结合成原子核或原子核分解为核子时,都伴随着巨大的能量变化,这个能量就是核能.原子核分解成核子时要吸收一定的能量,反之,根据能量守恒定律,核子结合成原子核时,也会放出同样多的能量.
二、结合能
我们考虑下面的问题。相距很远的两个物体,由于万有引力而相互接近,运动速度越来越大,引力势能转化为动能。最后撞在一起,一部分动能变成热并散失掉了。两个物体为了结合而付出了代价——失去了一些能量,如果要把它们分开,还要重新赋予它们能量。
类似地,要使基态氢原子电离,也就是要从氢原子中把电子剥离,需要通过碰撞、施加电场、让氢原子吸收光子等途径使它得到相应的能量(13.6eV),这个能量实际上就是电子与氢原子核的结合能,不过我们把它叫做氢原子的电离能,而结合能一词通常只用在原子核中。
☞如图,氦原子核是由两个质子和两个中子凭借核力结合在一起的,要把它们分开,需要吸收能量。反过来,4个核子结合成氦原子核要放出能量。那么,把核子分开需要的能量与核子结合放出的能量有什么关系?
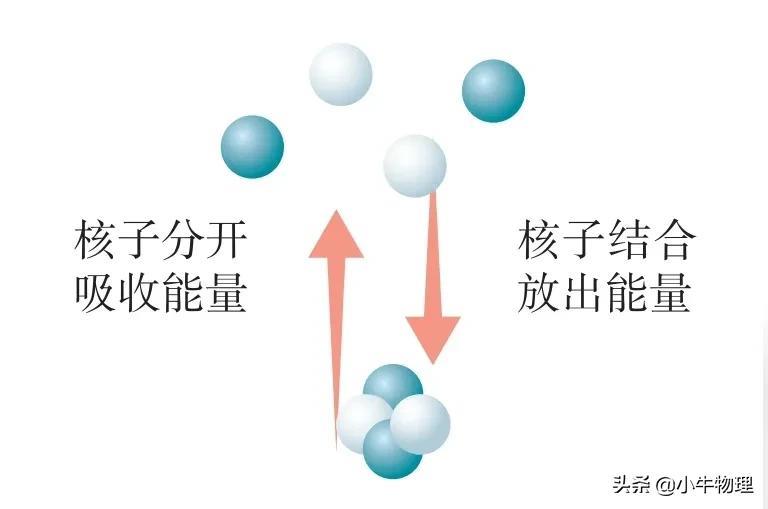
原子核是核子凭借核力结合在一起构成的,要把它们分开,也需要能量,这就是原子核的结合能(bindingenergy)。这个能量也是核子结合成原子核而释放的能量。
结合能的定义
从结合的角度定义:自由核子结合成原子核的过程中释放出来的能量,叫做该原子核的结合能.
从分解的角度定义:将原子核分解成自由核子时所需要的最小的能量,叫做该原子核的结合能.
由能量守恒定律可知,上述两个定义是一致的,在一个原子核的基础上,再结合一些核子,从而形成更大的原子核时,将进一步释放能量,因此原子核越大,其结合能越大.
☞类比化学键键能
三、比结合能
自然,组成原子核的核子越多,它的结合能越大。原子核的结合能与核子数之比,称做比结合能(specific binding energy),也叫作平均结合能。比结合能越大,原子核中核子结合得越牢固,原子核越稳定。
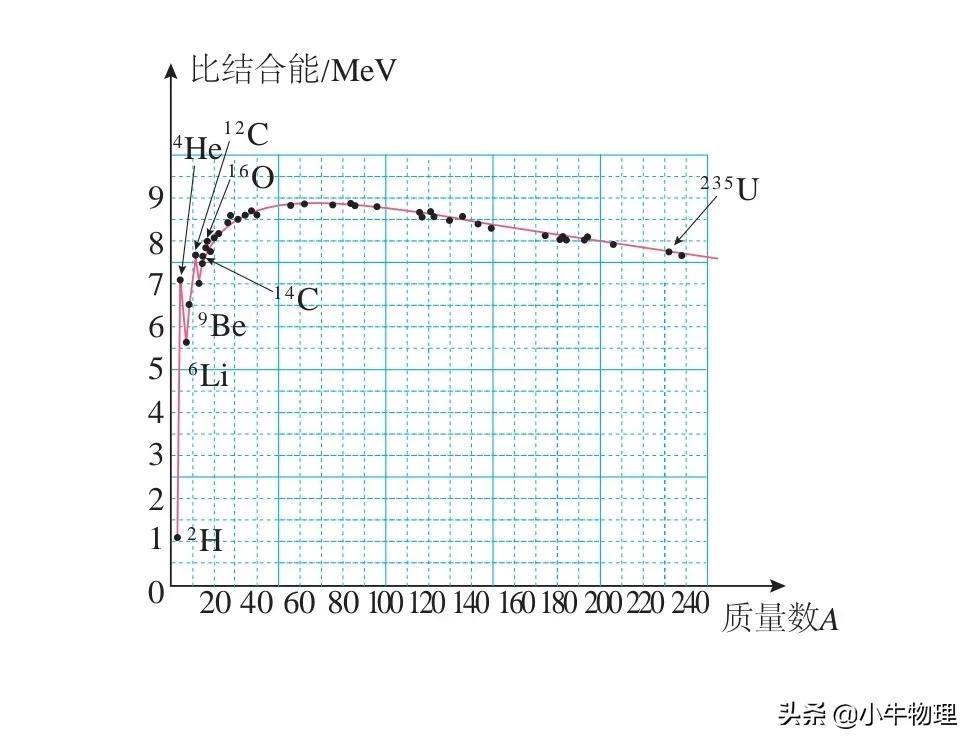
(1)比结合能曲线
不同的原子核,其比结合能不一样。右图为不同原子核的比结合能随原子序数变化的大致曲线,其中,⁵⁶₂₆Fe原子核的比结合能最大。
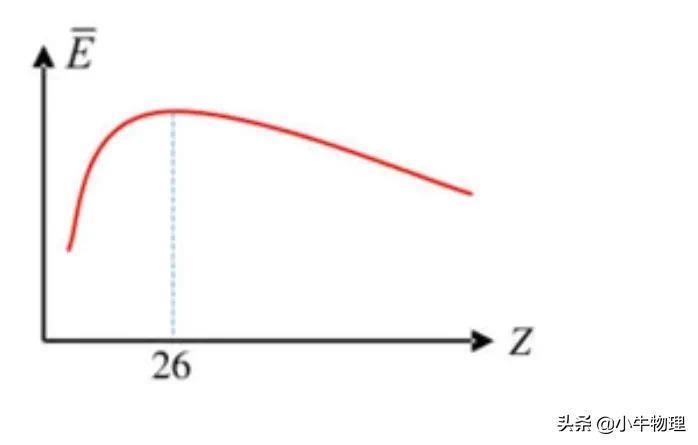
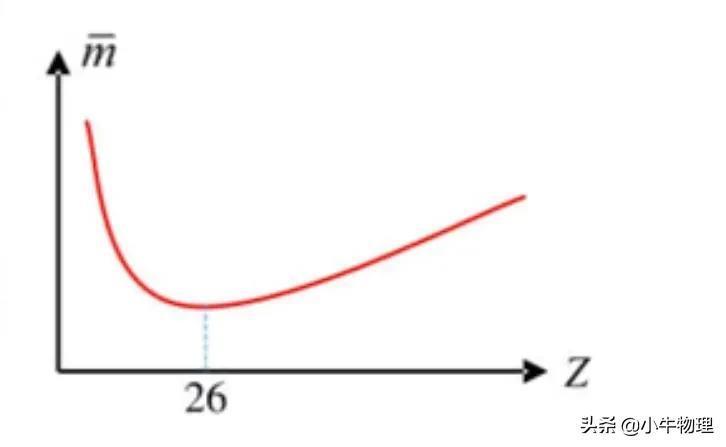
(2)平均核子质量曲线
比结合能,就是平均每个核子释放出来的能量,释放出来的越多,平均每个核子剩下的能量就越少,由E=mc²可知,平均每个核子的质量也就越小,如右图所示,其中⁵⁶₂₆Fe原子核的平均核子质量最小。
可以得出:①质量中等的核,比结合能量最大,约8.6MeV,它们最为稳定,重核的比结合能要小些,约7.6MeV,轻核的比结合能也要小些,并有明显的起伏,中等核有较大的比结合能,比邻近的核更为稳定。使重核裂变为两个质量中等的核或使轻核聚变,都可使核更为稳定并放出能量,这是核能释放的两种途径。②A>30以上的核,质量数变化较大,而比结合能变化不大,说明核的结合能差不多与质量数A成正比,显示核力的饱和性。这是因为核力是一种短程力,当A到达一定大小时,在核内和一个核子紧靠的核子数也根本不变,因此,比结合能也就根本稳定下来。核内质子之间有库仑力作用。这里和核力不同,为长程力。
因此,一个质子要受到核内所有其他质子的作用。当质子数增大时,库仑利的效果渐趋显著。这斥力有减小结合能的作用,这就是随着质子数的增加,比结合能又逐渐减小的原因。为了增加核的稳定性,在增加质子数的同时,多增加一些中子得会使核更稳定。其实,任何由更小的粒子组成系统的质量都小于组成粒子分散时的质量总和,都有相应的结合能。电子与原子核结合成原子的结合能就是原子的电离能,原子或离子结合成晶体也有结合能。核结合能比原子结合能要大得多。比结核能是原子核的结合能与该原子核所含有的核子数之比。
平均结合能的计算公式
某原子核的平均结合能=总结合能÷该原子核中的核子数
☞结合能可理解为把原子核中的所有粒子打散到无穷远处所需的能量。
平均结合能越大,原子核越难被分解成单个的粒子。
此外,平均结合能还具有以下特点:
1、重核的平均结合能比中核小,因此,它们容易发生裂变并放出能量。
2、轻核的平均结合能比稍重的核的平均结合能小,因此,当轻核发生聚变时会放出能量。3、铁的平均结合能最大。因此,比铁轻的原子多能聚变最终变为铁原子,比铁重的原子多能裂变最终变为铁原子。在大多数恒星的内部无法通过裂变或聚变获得能量的铁核。
4、氘的平均结合能与铁的平均结合能的差值比铀235的平均结合能与铁的平均结合能的差值要大好几倍。因此,核聚变释放的能量通常要比核裂变释放的能量大。
例题:下列说法正确的是( )
A.组成原子核的核子越多,原子核越稳定
B.原子核中所有核子单独存在时质量总和大于该原子核的总质量。
C.原子核中所有核子单独存在时的质量的总和大于该原子核的总质量
D.中子和质子合成氘核,若该过程质量亏损为△E=△mc²,则氘核的结合能为
例题:恒星向外辐射的能量来自其内部发生的各种热核反应,已知氘核(²₁H)的平均结合能为E₁,氦核(⁴₂He)的平均结合能为E₂,则热核反应²₁H+²₁H→⁴₂He释放的能量为()
A.E₂-E₁
B.E₂-2E₁
C.4E₂-2E₁
D.4E₂-4E₁
根据不同的已知条件通常可以有两种计算方法
方法一:利用质量亏损计算
先查出氘核和氦核的质量 m=2.014102u,me=4.002603u 然后根据反应前后的质量亏损用质能方程算出释放的核能
方法二:利用比结合能计算
先查出氘核和氦核的结合能
ED=1.11MeV. EHe =7.07MeV. 然后采用“先拆散、后结合”的方法即先把2个氘核分解成4个自由核子(2个中子和2个质子)使这4个自由核子结合成核比较前后两个过程中释放的结合能同样可得出结果 如方法一核反应前后的质量亏损为 △m=2md-mHe=2×2.014102u-4.002603u =0.025601u. 释放出的核能为
△E=0.025601×931.5MeV=23.8473315MeV
解析:热核反应是两个氘核聚变为氦核,根据能量守恒可知,该热核反应释放的能量为△E=4E₂-4E₁,选项D正确。